Artificial intelligence has been used by Bayreuth scientists to create a new approach to investigating liquid and soft materials. Their “neural functional theory” opens a new chapter in density functional theory, as reported in a paper that was just published in the esteemed journal Proceedings of the National Academy of Sciences of the United States of America (PNAS).
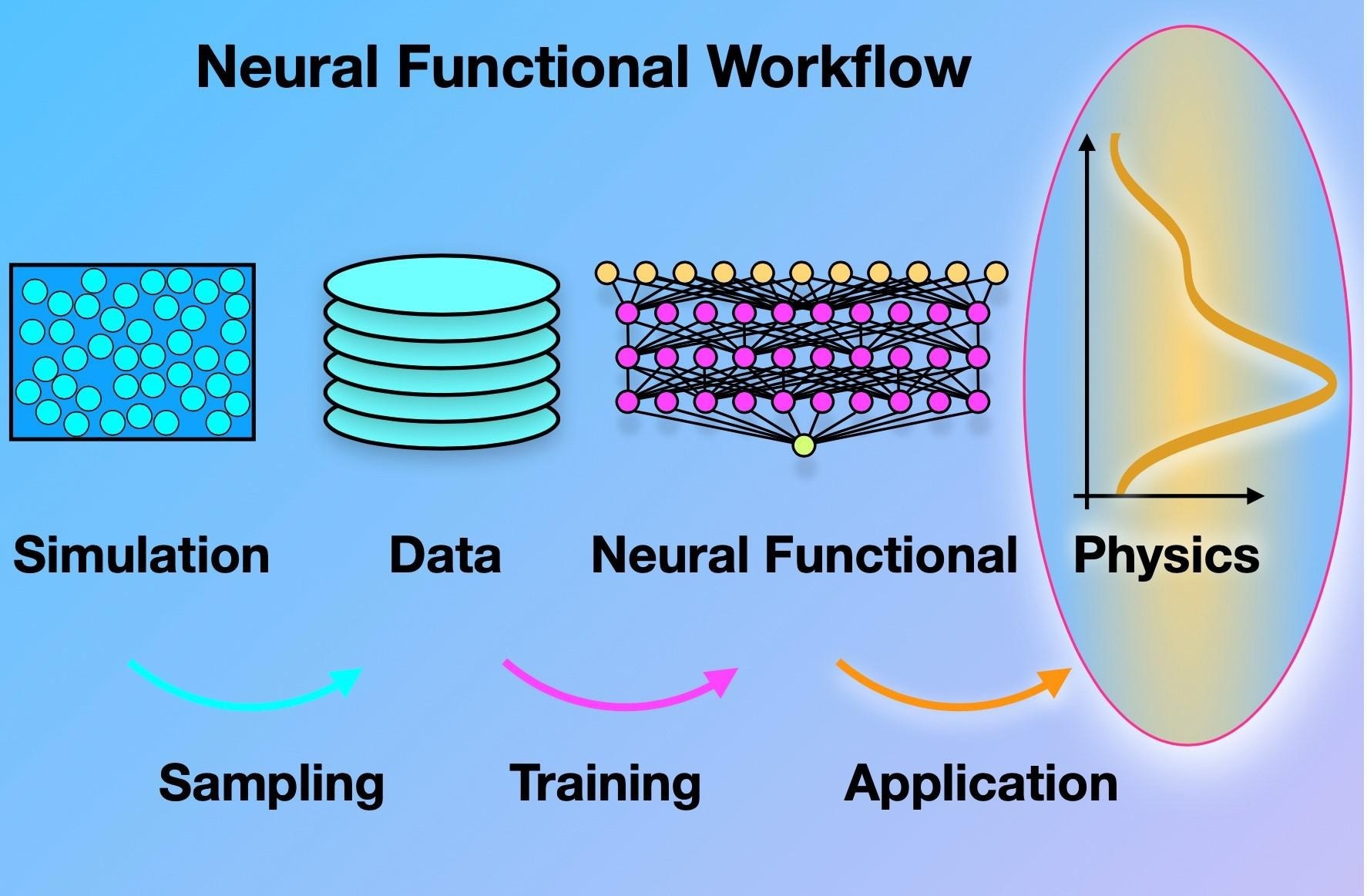
The illustration shows the workflow inherent in the neural functional theory, starting with data acquisition via sampling in particle-based computer simulations. A neural network is trained to represent direct correlations that are intrinsic to the physical system at hand. The theory can then be freely applied to real physical problems, more quickly and in greater depth than what was possible before. Image Credit: UBT
Humans live in a highly technologically advanced society with a complex network of interdependencies and interactions between individuals, where fundamental research catalyzes innovation. The study that has been published offers fresh approaches that might significantly impact popular simulation methodologies, enabling more rapid, accurate, and thorough computer investigations of complicated materials.
This could influence the design of products and processes in the future. The accurate representation of liquid structure by the recently developed neural mathematical connections is a significant advance that provides a multitude of opportunities for obtaining profound scientific understandings.
In the study, we demonstrate how artificial intelligence can be used to carry out fundamental theoretical physics that addresses the behavior of fluids and other complex soft matter systems. We have developed an advanced scientific method to study matter at the atomic and (macro)molecular level, combining machine learning and mathematical methods to calculate complex physical properties.
Prof. Dr Matthias Schmidt, Chair, Theoretical Physics II, University of Bayreuth
The Bayreuth researchers describe a hybrid approach to calculate the equilibrium structure and thermodynamics of fluids under various conditions, based on classical density functional theory and machine learning.
Schmidt added, “We demonstrate the use of the neural functional in the self-consistent computation of density profiles. The quality of the results exceeds the state of the art of fundamental-measure density functional theory. The results establish machine learning of functionals as an efficient tool for the multiscale description of soft matter.”
Thus, a basic understanding of the composition of matter is obtained. This kind of material could become commonplace, but it can also be used as the foundation for industrial operations and consumer goods.
“This powerful combination of essentially simple basic techniques has opened a new chapter in density functional theory because networks trained by simulation data are more accurate than the currently best theoretical approximations designed ‘by hand'’, i.e. with paper and pencil,” Schmidt further added.
He emphasized, “In addition to the significance for the particular field of statistical mechanics of soft matter, I think our method also raises fundamental questions about the human self-understanding of our intellectual activity. For myself, our study gives considerable hope for developments where artificial intelligence, rather than replacing us, expands us in a way that I find very surprising.”
The research was supported by funding from a DFG project.
To go along with the PNAS study, the University of Bayreuth researchers have also provided widely accessible tutorial material. This contains an additional introductory article (“Why neural functionals suit statistical mechanics” by Florian Sammüller, Sophie Hermann, and Matthias Schmidt) and code that can be accessed and used online by interested parties.
Journal Reference
Sammüller, F., et. al. (2023) Neural functional theory for inhomogeneous fluids: Fundamentals and applications. Proceedings of the National Academy of Sciences of the United States of America. doi:10.1073/pnas.2312484120